Sum to Infinity Geometric Progression

What is the sum of infinite geometric progression. Q1 Find the sum to infinity of the Geometric Progression 5 4 5 16 5 64 5 256.

Proof Of The Geometric Series Formula Finite Infinite Youtube

A 1 R -025.

. Please try your approach on IDE first before moving on to the solution. But the thing is when my teacher asked my class what we would expect the. The sum of the geometric series refers to the sum of a finite number of terms of the geometric series.

Solved Example on Sum of Infinite GP. R is the common ratio between each term in the series. The given problem can be solved based on the following observations.

3232r1-r5 31 - 31r 1r -32r5 32r6. Lets examine the sum to infinity of a couple of examples then generalise. It has first term a 5 4 and the common ratio r 1 4 Also r 1.

Here we have studied the sum of infinite terms of the geometric series by using solved examples that will help understand the concept easily. Tutorial on Geometric series. 341 frac13 The sum of.

Sum to infinity of the geometric progression. A geometric series can be finite or infinite as there are a countable or uncountable number of terms in the series. Now click the button Calculate to get the sum.

The procedure to use the infinite geometric series calculator is as follows. The first term of T and the first term of U are each 4. In order the first three terms of the combined series S are 8 3 and 54.

Enter the first term and common ratio in the respective input field. If absolute of value of R is greater than equal to 1 then the sum will be infinite. The infinite sum of an infinite geometric series formula is often infinity either positive or negative infinity.

The series 4 7 10 13 16 also diverges. A geometric series is a series where each subsequent number is obtained by multiplying or dividing the number preceding it. Answer 1 of 7.

Answer 1 of 2. Otherwise the sum of the Geometric series with infinite. Only when a certain condition is met will the infinite sum result in a calculable.

I know that the geometric distribution follows the rules of a geometric progression thus by using the sum to infinity formula which I know its proof and is really convinced by it a 1 r. Solved examples to find the sum to infinity of the Geometric Progression. We can easily arrive at this.

Therefore the sum to infinity is given by. For the geometric progression aarar2ar3 ldots ldots. Is 341 The sum of.

The sum of an infinite Geometric Progression with first term a and common ratio r -1 r 1 ie r 1 is S a1 - r Sum of an infinite Geometric Progression. P 1 1 p p 1 1 p p p 1. A1 The given Geometric Progression is 5 4 5 16 5 64 5 256.

The sum to infinity of a geometric series. This is only possible however if the terms in the series are decreasing in size. Sum to Infinity of a Geometric Sequence.

It is given that a_0 frac 11-r 32 and a_0 frac 1-r51-r 31 Multiplying both sides of each equation by frac 1-r1-r. First we need to be OK with the following. This means that we may allow the terms to continue to be added forever.

Finally the sum of the infinite geometric. What is the sum to infinity of S. Frequently Asked Questions FAQs Q1.

Finite Sum to Infinity of a Geometric SeriesThis example shows how to calculate the finite sum to infinity of a given geometric seriesLeaving Cert Maths HL. When and then the sequence converges to zero regardless of the first term Although doesnt generate a very interesting sequence. Learn the Concepts on Sequences and Series.

Unlike with arithmetic series it is possible to take the sum to infinity with a geometric series. It follows that it is possible to take the sum to infinity when the common ratio is between. We get a_0 32 - 32r for the first which we can substitute into the second.

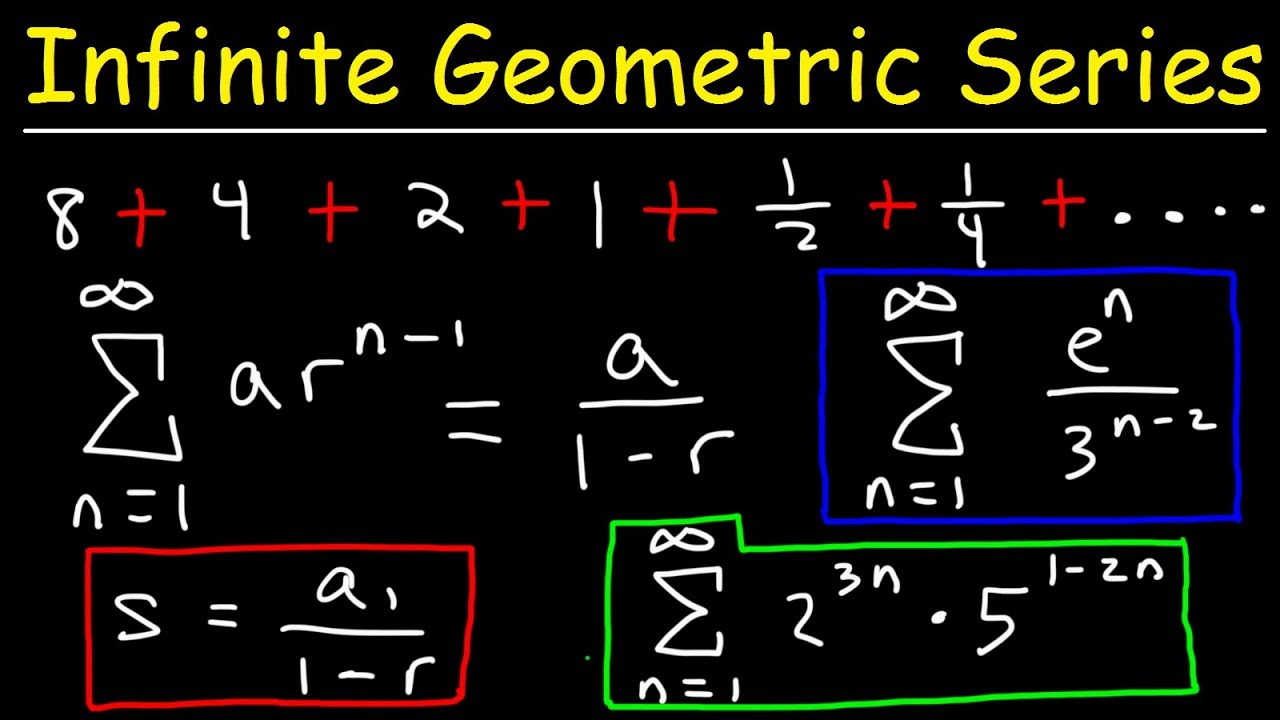
Subscribe for more math t. A 1 is the first term in the series. The sum to infinity of a geometric series is given by the formula Sa1 1-r where a1 is the first term in the series and r is found by dividing any term by the term immediately before it.

A Level Pure This video explains how the sum to infinity of a geometric series is derived and how to calculate the sum to infinity. The terms of an infinite series S are formed by adding together the corresponding terms in two infinite geometric series T and U. Sum of Geometric Series.

Geometric Series Sum To Infinity Examsolutions Youtube

Calculus Formula For Finding A Sum Of Series Sum K 0 Otosection

Prove The Infinite Geometric Series Formula Sum Ar N A 1 R Youtube

Finding The Sum Of An Infinite Geometric Series Youtube